Equações e cálculos do paraquedas de minifoguetes
Fonte:
Fudação Cecierj / Consórcio Cederj
Como funciona o paraquedas?
O princípio básico de funcionamento de um paraquedas é aumentar a área de um objeto em queda, criando um sistema com grande área em contato com o ar, diminuindo com isso a velocidade de retorno do objeto ao solo. Do ponto de vista físico, há dois elementos fundamentais que compõem esse cenário: a força de gravidade e a força de arrasto. A força de arrasto, devida à resistência do ar, faz resistência ao movimento descendente do objeto, isto é, a força de arrasto opõe-se à direção da velocidade.
Um cálculo preciso da força de arrasto é um tanto complicado e não existe uma “lei geral” que possa ser utilizada em todas as situações em que haja resistência gerada pelo ar. Entretanto, uma boa estimativa da magnitude da força de arrasto devida à resistência do ar, aqui denotada por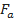 
, agindo sobre o sistema objeto-paraquedas, pode ser dada por
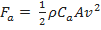 | (1), |
em que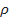 
representa a densidade do ar (unidade: 
, 
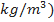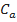representa o coeficiente de arrasto (é uma grandeza adimensional), 
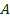representa a área exposta do velame do paraquedas (unidade: 
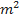) e 
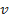representa a velocidade descendente do objeto (unidade: 
).
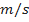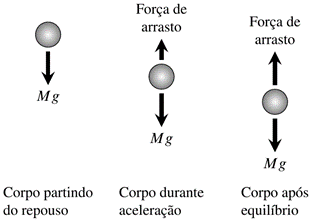
Figura 2: Diagrama de forças agindo sobre o objeto durante a queda
A equação (1) mostra que, quando o objeto inicia o movimento de descida, após atingir o apogeu, a força de arrasto pode ser negligenciada, já que a velocidade nesse momento é pequena. Por outro lado, à medida que a velocidade do objeto é maior, a força de arrasto passa a ser significativa. Considerando-se o movimento ao longo da direção vertical e assumindo a aceleração da gravidade positiva para um corpo em queda, a Segunda Lei de Newton assegura que:
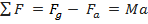 | (2). |
Dessa forma,
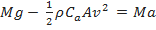 | (3), |
onde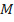 
representa a massa total do sistema objeto-paraquedas, 
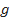é a aceleração da gravidade e 
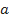é a aceleração resultante do sistema. Em algum momento, a força de arrasto será (aproximadamente) igual ao peso do sistema objeto-paraquedas. Assim, a aceleração resultante é quase nula, de modo que a velocidade final 
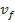será atingida e (praticamente) constante.
Quão grande deve ser o paraquedas?
A área da seção transversal do velame do paraquedas, em função da velocidade final, é dada por:
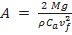 | (4). |
Figura 3: O velame é a parte superior, na cor cinza
Fonte: Estes Rocket Factory.
Daqui em diante, admite-se que o velame do paraquedas tem seção transversal circular de diâmetro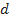 
. Uma vez escolhida a velocidade final adequada para o retorno do objeto ao solo em segurança, o diâmetro 
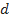passa a ser função exclusivamente da massa 
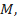pois todos os outros parâmetros são conhecidos. Assim, tem-se
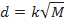 | (5), |
com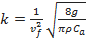
.
É natural pensar que melhores resultados serão obtidos ao se construir um paraquedas com área muito grande. De fato, a equação (4) enseja que, quanto menor for a velocidade final desejada, maior deverá ser a área do velame a ser utilizado. Entretanto, há dois inconvenientes imediatos na prática dessa ideia. O primeiro se deve ao fato de que há limitações de espaço no compartimento destinado a alojar o paraquedas. Já o segundo é proveniente do fato de que, quanto maior for a área do paraquedas e quanto mais tempo o objeto estiver no ar em queda, maior é a possibilidade de o vento empurrar o objeto para longe de onde se deseja pousar.
Assim, idealmente, o paraquedas deve ter tamanho adequado para que o objeto tenha um pouso suave e, ao mesmo tempo, retorne ao solo num tempo razoável.
Cálculo do diâmetro: minifoguetes
O foguetemodelismo é a prática de projetar, construir e lançar minifoguetes. São modelos geralmente de pequena escala que utilizam uma plataforma de lançamento e acessórios tais como sistema de disparo e motores a pólvora negra. Geralmente são recuperados por meio de paraquedas, dentre outros modos de recuperação. Apesar de o hobby de lançar minifoguetes existir desde o início do século XX, sua prática se popularizou fortemente somente após o lançamento do primeiro satélite artificial (o Sputnik 1) pela União Soviética em 1957. A partir daí, o tema espacial virou uma verdadeira febre, incentivando principalmente os jovens a praticar o foguetemodelismo. Na mesma época, nos Estados Unidos, era fundada a empresa Estes de foguetemodelismo, que, pela primeira vez, produziu minifoguetes em grande escala e com segurança, além de kits e uma série de acessórios necessários para a prática.
Quando se deseja utilizar o paraquedas como método de recuperação do foguete, é possível utilizar as fórmulas apresentadas antes para determinar o tamanho que o paraquedas deve ter em função dos parâmetros do foguete e do próprio paraquedas e da velocidade final que se deseja. Essa é uma boa aplicação que ilustra o uso do conceito matemático de função – a obtenção de um valor final (diâmetro do paraquedas) que corresponderá aos parâmetros desejados. Outra questão relacionada é como efetivamente calcular o valor da função em termos dos parâmetros; para isso, o computador pode ser de grande ajuda, como veremos adiante.
Nesta seção, utilizando dados de modelos de minifoguetes comercializados, serão apresentados os resultados do cálculo do diâmetro dos velames de paraquedas do sistema de recuperação. Esses resultados são obtidos em função da massa do foguete, pois a velocidade final é fixada normalmente, definida de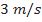 
a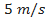
. No que se segue, será assumido que 
, 
, 
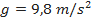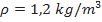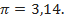Além disso, os velames considerados são de dois tipos: planos ou em forma de cúpula (hemisfério).
Tabela 1
| Velame plano | Velocidade final | |||
Coeficiente de arrasto:  |  |  | ||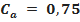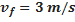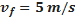
| Modelo | Fabricante | Massa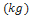 | Diâmetro ( | |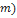
| Red Nova | Estes Rocketry |  |  |  |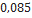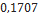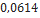
| 17266 295 Mean | Estes Rocketry |  |  |  |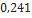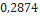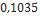
| InterrMachineogator-G | Sirius Rocketry |  |  |  |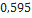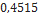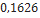
| Hi-Tech | LOC Precision Rocketry |  |  |  |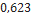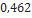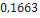
| Space Ark | Pemberton Technology | 0,790 |  |  |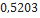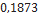
| Hawk mim 23-B | Madcow Rocketry |  |  |  |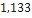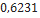
| Tomach (2.6” DIA) | Madcow Rocketry |  |  |  |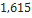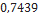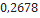
| Black Brant II | Madcow Rocketry |  |  |  |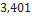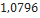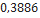
Tabela 2
| Velame hemisférico | Velocidade final | |||
Coeficiente de arrasto:  |  |  | ||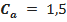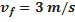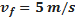
| Modelo | Fabricante | Massa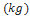 | Diâmetro ( | |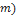
| Red Nova | Estes Rocketry |  |  |  |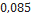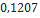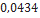
| 17266 295 Mean | Estes Rocketry |  |  |  |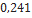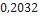
| InterrMachineogator-G | Sirius Rocketry |  |  |  |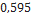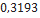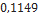
| Hi-Tech | LOC Precision Rocketry |  |  |  |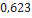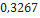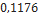
| Space Ark | Pemberton Technology | 0,790 |  |  |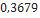
| Hawk mim 23-B | Madcow Rocketry |  |  |  |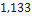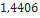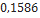
| Tomach (2.6” DIA) | Madcow Rocketry |  |  |  |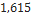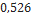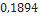
| Black Brant II | Madcow Rocketry |  |  |  |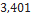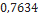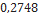
Discussão: qual o papel do computador?
Ao observar as Tabelas 1 e 2, nota-se que o cálculo dos valores da expressão do diâmetro (isto é,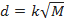 
) não é trivialmente realizado. É hora de apelar ao computador! O professor terá a oportunidade de alertar os estudantes sobre como o computador pode ser útil em situações reais e artificiais como as normalmente apresentadas nos textos. Qualquer software gratuito, imediatamente acessível a professores e alunos, poderá, por meio de programação elementar, fornecer muito rapidamente os resultados das tabelas. Um dos softwares mais populares e fáceis de utilizar é o GeoGebra; entre diversas outras aplicações, ele pode ser usado para o cálculo de funções que o usuário determina via fórmulas matemáticas.